Calculs pratiques au CE2. Situations concrètes et observations de l’environnement

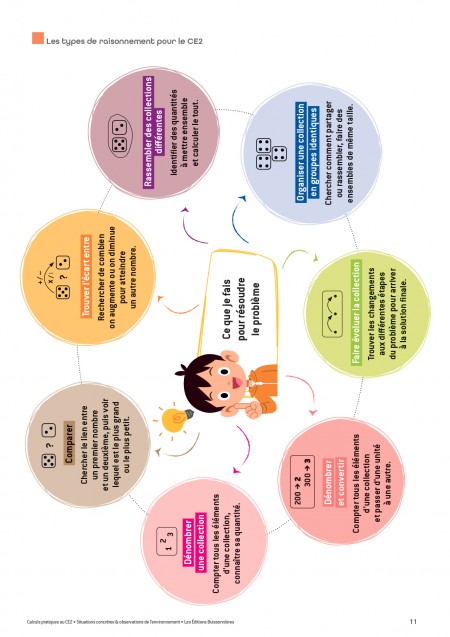
Calculs pratiques au CE2 est le troisième fichier d’une série qui a pour objectif d’entraîner les élèves du cycle 2 à la résolution de problèmes avec une méthode suscitant leur intérêt et bien structurée sur le fond pour favoriser les apprentissages. 

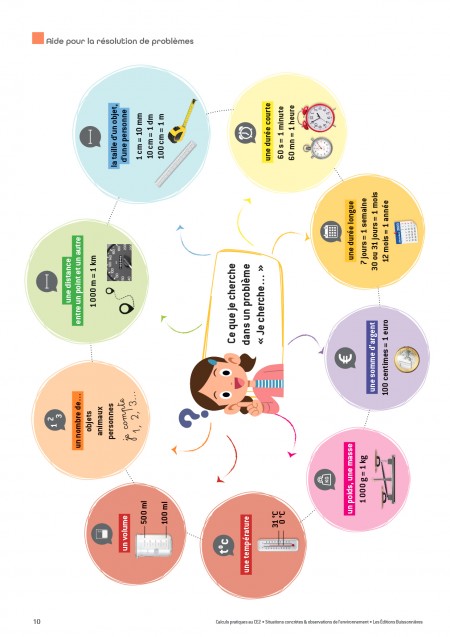
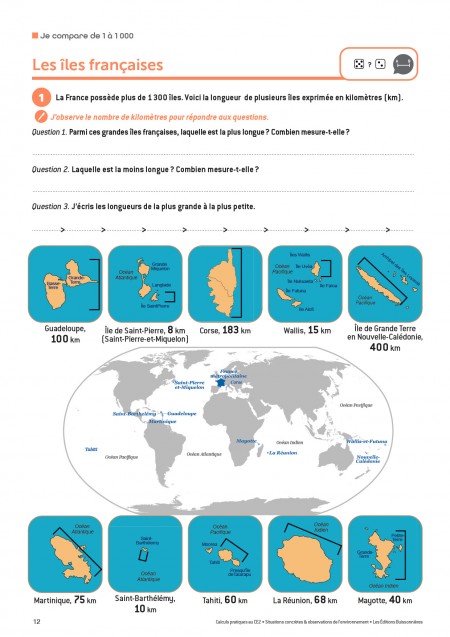
Les sujets choisis pour ces problèmes ont du sens et correspondent aux centres d’intérêt des enfants : la nature, les animaux, le sport, le corps humain, la solidarité, le développement durable, l’agriculture, les livres, les transports… Les situations abordées sont proches du vécu des enfants. Elles sont rendues plus concrètes encore par des illustrations explicites rigoureusement choisies. Cela leur permet de bien s’approprier la situation afin de faciliter le raisonnement. 

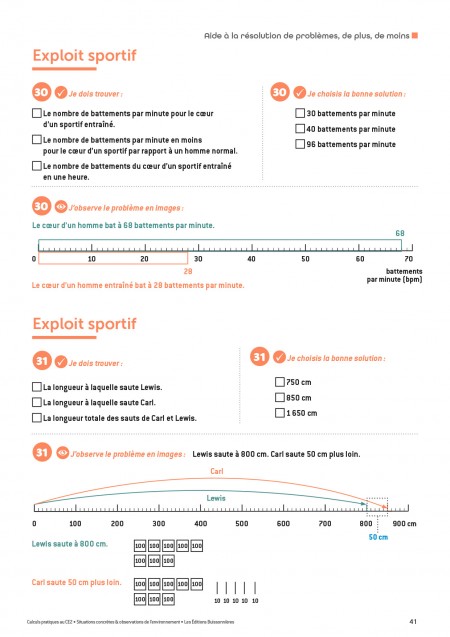
Le fichier regroupe 81 exercices : il est donc possible d’en faire travailler deux ou trois par semaine. Les fiches comportent souvent deux exercices (pour appliquer à nouveau le modèle de raisonnement une fois le premier problème résolu), complétés par une page d’aides que l’enseignant choisira de donner aux élèves qui en ont besoin. 

In fine, l’objectif pédagogique poursuivi dans cet ouvrage et sa démarche est d’aider chaque élève à se rendre compte de ce que représente le nombre. La réalisation de ces fiches contribue à lui donner des références utiles toute la vie : la taille d’un enfant, d’un adulte, d’un animal à plusieurs étapes de sa vie, d’un monument ; le prix, la dimension ou le poids d’objets usuels, la durée de morceaux de musique… 

« Sous prétexte de faire des maths, j’ambitionne surtout de transmettre une culture très riche à chaque élève. » Francine Moyne, enseignante-autrice